算法学习之希尔排序

jiayao 收录于编程算法

2021-04-28 约 1553 字预计阅读 4 分钟

本文是学习排序系列的第二篇，主要介绍插入排序的进阶版->希尔排序

注：本文的排序算法默认升序

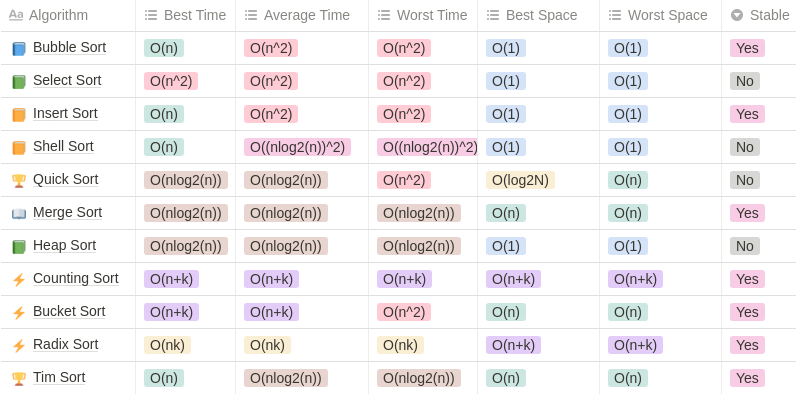
0. 常见排序算法性能对比

再贴一张常见排序算法的性能对比，方便查看~

1. 希尔排序(`插入`)(`In-place`)

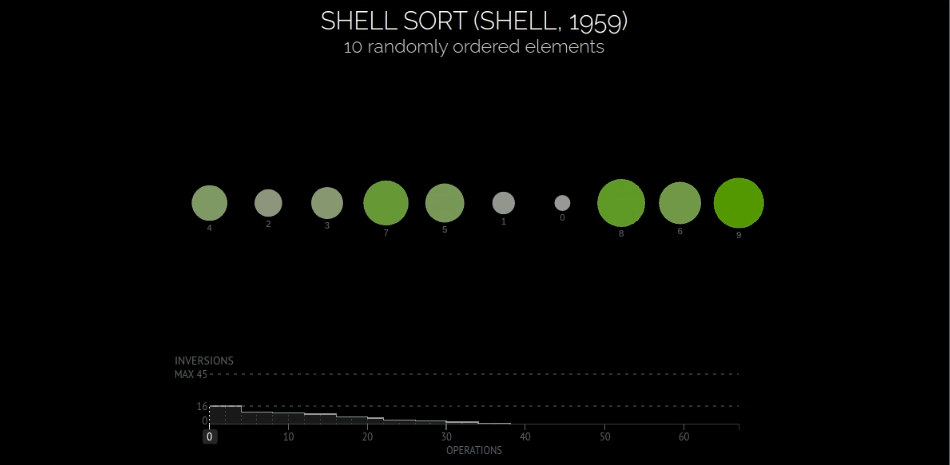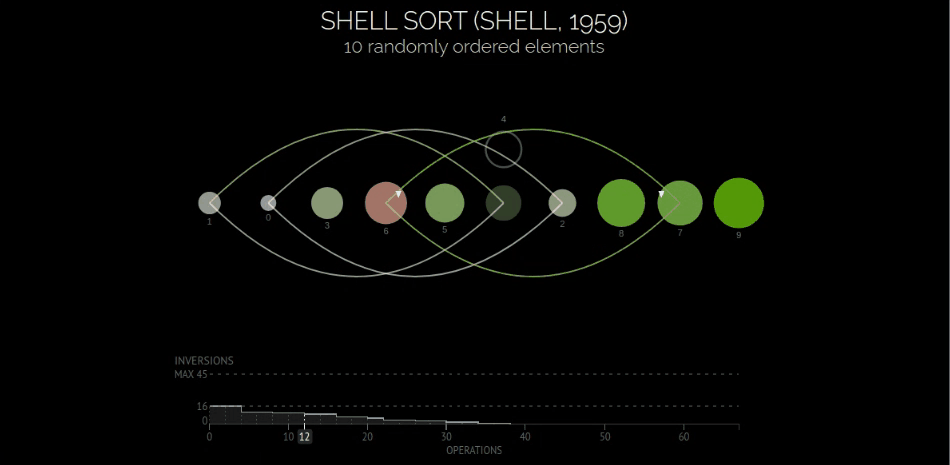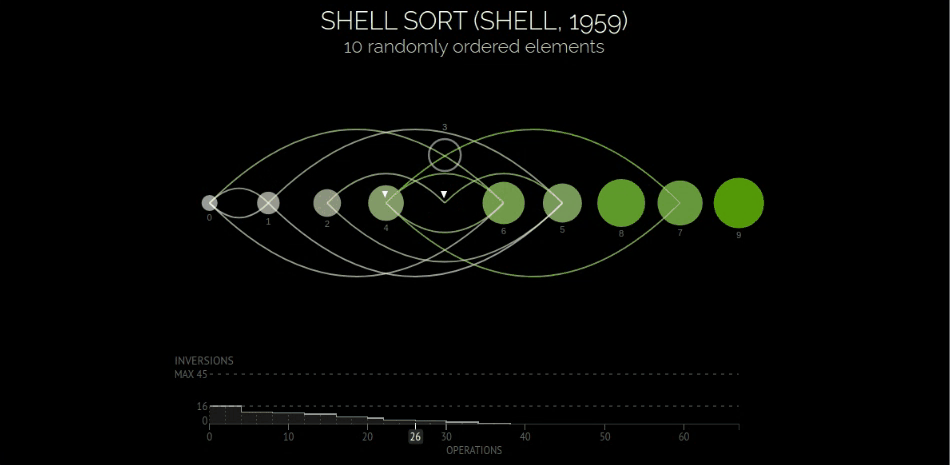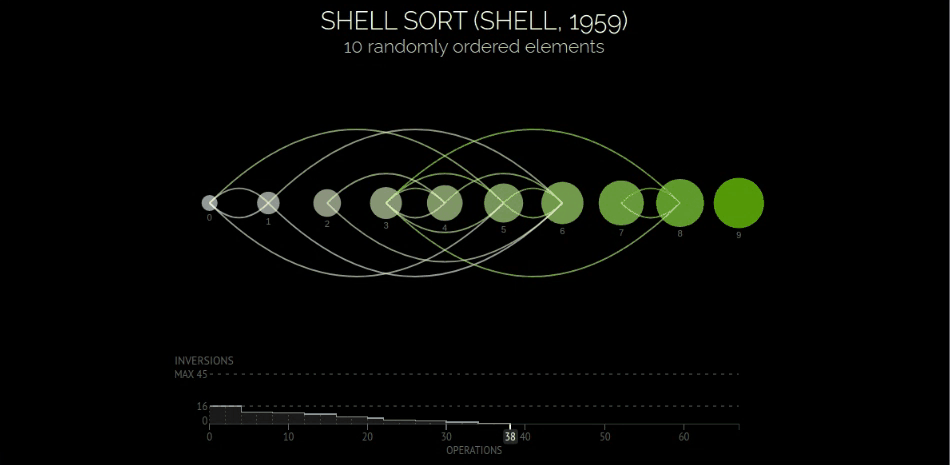
定义与可视化

希尔排序也叫递减增量排序，其在直接插入排序的基础上，巧妙使用增量的概念，让插入排序的作用对象逐层有序，而递减增量指的是增量的数值依次减小最终为1

定义(人话版)

OK，说人话，上一篇总结了插入排序的原理和特点，我们知道插入排序在输入序列基本有序的情况下是蛮快的，时间复杂度可以达到O(N)级别，只不过插入排序针对基本逆序的输入处理依旧不够简洁。那么希尔排序，则是插入排序的升级版，通过预处理+插入排序的方案，最优情况下可以达到O(N)的时间复杂度。输入不够有序？先处理成相对有序，再进行插入排序操作就好~

那么具体如何实现呢？希尔排序中用到了一个名词，叫做增量，记做gap，这个增量的作用是将原输入序列分批，与其直接处理原输入，先处理第1个元素与第gap+1个元素，将二者作为一组进行插入排序，原数组不够有序？其实减小输入规模，也相当于间接地减小无序程度。此外，希尔排序的定义中为什么说递减增量呢？其实换个角度理解，增量越大，每批处理的元素越多，那么增量递减相当于逐渐增加插入排序每次处理的数据规模，而且当前的数据又是在上一个增量时已经提前预处理过了，所以插入排序处理起来会更简单。

增量设定&如何递减

最简单的增量方案(折半)

我们先以折半的方案为例，熟悉希尔排序的具体操作过程，便于写代码实现

首先，给定一些定义，我们设定增量为gap，输入序列长度为N，gap初始值为N//2
根据gap的值进行分批插入排序
- 遍历的起止索引是gap -> (len(N)-1)
- 当前索引如果是cur，那么当前批的索引是
  
  …, cur-3gap, cur-2gap, cur-gap, cur
  
  将当前批索引对应的元素进行插入排序
- 将索引cur右移一位，重复上一过程
更新gap的值为 gap = gap//2
gap为0时，遍历结束

在上述过程中，折半增量的作用就是每次都将插入排序的对象数量扩大一倍，而且扩大前后的两批数据并不是相互独立的，而是扩大前的数据已经是有序的。一直到最后，gap为1时，插入排序拿到的数据已经是近乎有序的了，这就是预处理的作用。

极端情况

折半增量虽然简单容易理解，但是存在一种极端的情况，那就是当gap的值等于1之前，可能每批数据都是有序的，这时gap=1，插入排序拿到的序列顺序与原始顺序一致，相当于gap等于1之前的操作都是额外的，这样反而比直接插入排序还要耗时

如上图，gap初始为4，然后为2，你会发现这两种情况对应的数据都已经是有序的。

造成这种情况的原因就是：增量方案不够严谨。事实上，希尔排序的时间复杂度的确取决于增量递减的方案，那么，为了保证分组粗调没有盲区，每一轮的增量需要彼此“互质”，也就是没有除1之外的公约数，这样才能保证希尔排序不会好心办坏事。

所以，为了使增量互质，人们又提出了Hibbard增量：2^k-1[1, 3, 7, 15, …]，后续还有很多其他方案被提出，不过这不是我们关注的重点了。

比较

相比于直接插入排序

希尔排序是不稳定的，数据交换过程中可能丢失稳定性
希尔排序的比较次数和移动次数比直接插入排序要少，N越大效果越明显
希尔排序中增量gap的取法必须满足最后一个步长为1

代码

以折半增量为例

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


def shellsort(nums: List) -> List:
    length = len(nums)
    gap = length

    while gap > 0:
        for i in range(gap, length):
            cur_val = nums[i]
            last_id = i - gap
            while last_id >= 0 and nums[last_id] > cur_val:
                nums[last_id + gap] = nums[last_id]
                last_id -= gap
            nums[last_id + gap] = cur_val
        gap //= 2

    return nums

复杂度分析

设定序列长度为N

时间复杂度

最坏时间复杂度为𝑂(𝑁^(3/2))，平均时间复杂度约为𝑂(𝑁^(5/4))
空间复杂度

因为是原地操作，所以空间复杂度为O(1)

稳定性分析

希尔排序是不稳定的，因为其在插入元素的过程中可能会交换相等元素的顺序。

可视化网站

SORTING

目录