本文是学习排序系列的第三篇,主要介绍归并排序
注:本文的排序算法默认升序
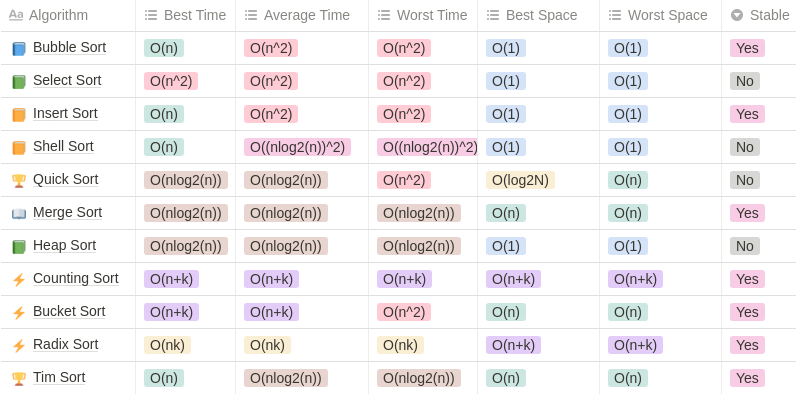
0. 常见排序算法性能对比
再贴一张常见排序算法的性能对比,方便查看~

1. 归并排序
定义与可视化
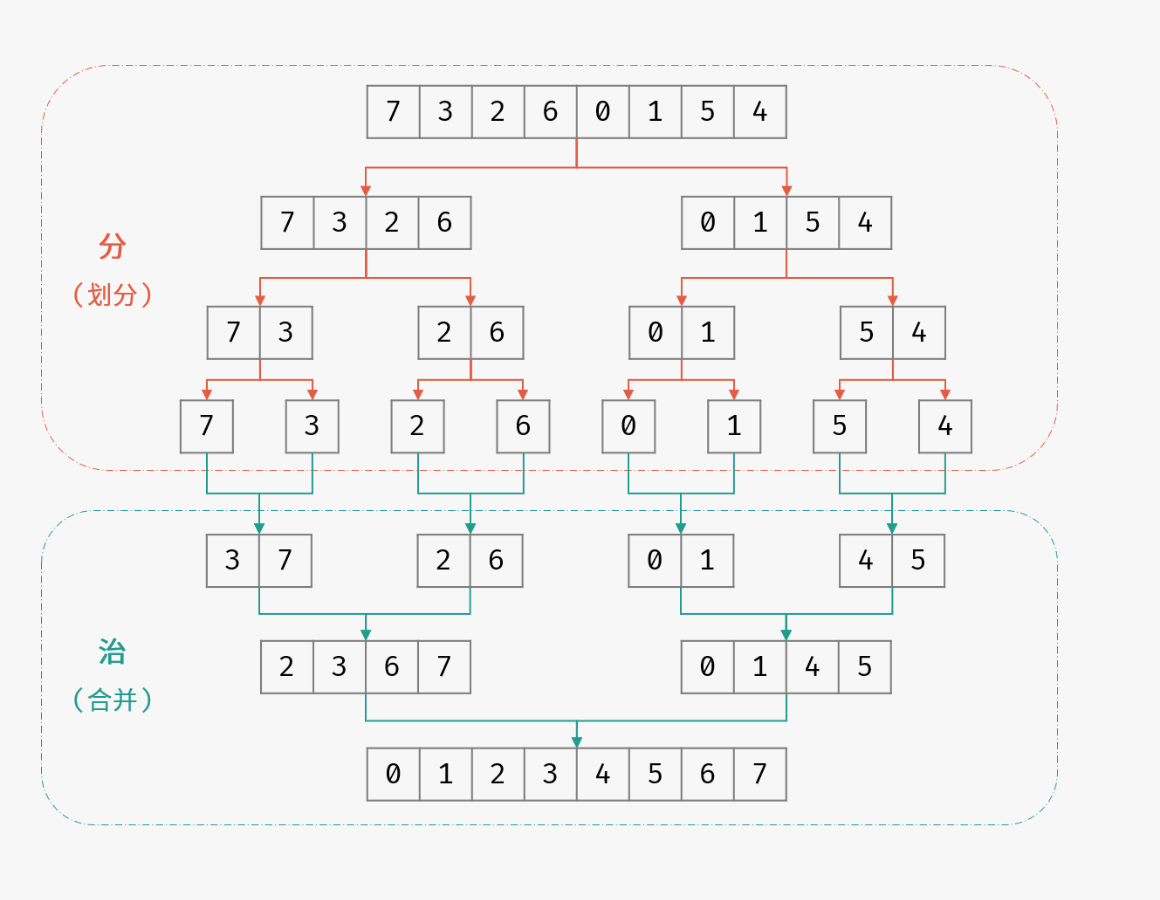
归并排序的算法思想是分治,即先将待排序的序列划分成若干子序列,对子序列排序,然后再合并子序列的排序结果。归并排序就是个二叉树的后序遍历

再放一张K神的图,比较清晰,来源

算法步骤
给定一个待排序的序列,归并排序将主要分为两步,拆分、合并:
-
将序列递归地分成两份,直到子序列的长度为2,拆分停止。如果序列总长度为奇数N,则一份是(N+1)/2,一份是(N-1)/2
-
对子序列进行合并,每个子序列的合并规则如下
定义两个指针,循环对比指针指向元素的大小,取较小的放入原数组,注意更新指针位置。循环停止条件是有一个指针走到了子序列的末尾,这时剩余元素一定是较大值,直接插入原数组后面即可。
代码
每次递归都将序列一份为二,直到当前序列长度小于或等于2,对两个元素进行比较交换,那么对于长度大于2的子序列,每次都会创建与原序列相同长度的空间,以作为临时的排序结果。python代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
def mergesort(nums: List) -> List:
def merge(arr_, left_, mid_, right_):
ptr1, ptr2, res_ = left_, mid_+1, []
# 遍历ptr1和ptr2,装填res_数组,直到ptr1或ptr2到头
for i in range(right_-left_+1):
if ptr1 > mid_ or ptr2 > right_:
break
if arr_[ptr1] <= arr_[ptr2]: # 注意 '=' 才能让排序稳定
res_.append(arr_[ptr1])
ptr1 += 1
else:
res_.append(arr_[ptr2])
ptr2 += 1
# 调用extend将剩余元素都装入数组res_中
if ptr1 > mid_:
res_.extend(arr_[ptr2:right_+1])
if ptr2 > right_:
res_.extend(arr_[ptr1:mid_+1])
# 替换arr_区间中对应的区域
arr_[left_:right_+1] = res_
def mergesort_rec(arr, left, right):
if left >= right:
return
mid = (right + left) // 2
mergesort_rec(arr, left, mid)
mergesort_rec(arr, mid+1, right)
merge(arr, left, mid, right)
length = len(nums)
mergesort_rec(nums, 0, length-1)
return nums
|
空间优化:
我们可以对空间进行优化,实际上一共迭代了log2(N)次, 每次空间占用最大就是N,所以可以创建一个长度与原序列相同的数组,这样就只需维护这一个数组即可,避免频繁开辟空间。当前序列长度小于N时,可以只使用一部分。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
def mergesort(nums: List) -> List:
def merge(arr_, left_, mid_, right_, tmp_):
ptr1, ptr2, index = left_, mid_+1, 0
# 遍历ptr1和ptr2,装填tmp数组,直到ptr1或ptr2到头
for i in range(right_-left_+1):
if ptr1 > mid_ or ptr2 > right_:
break
if arr_[ptr1] <= arr_[ptr2]: # 注意 '=' 才能让排序稳定
tmp_[index] = arr_[ptr1]
ptr1, index = ptr1+1, index+1
else:
tmp_[index] = arr_[ptr2]
ptr2, index = ptr2+1, index+1
# 调用extend将剩余元素都装入数组tmp中
if ptr1 > mid_:
tmp_[index:right_-left_+1] = arr_[ptr2:right_+1]
if ptr2 > right_:
tmp_[index:right_-left_+1] = arr_[ptr1:mid_+1]
# 改变arr_区间中的元素顺序
arr_[left_:right_+1] = tmp_[:right_-left_+1]
def mergesort_rec(arr, left, right, tmp):
if left >= right:
return
mid = (right + left) // 2
mergesort_rec(arr, left, mid, tmp)
mergesort_rec(arr, mid+1, right, tmp)
merge(arr, left, mid, right, tmp)
length = len(nums)
mergesort_rec(nums, 0, length-1, [0]*length)
return nums
|
归并排序特点
- 归并排序的时间复杂度与空间复杂度和原序列是否有序无关
复杂度分析
设定序列长度为N
稳定性分析
归并排序是稳定的,因为在比较时,对于相等的元素,优先采用索引较小的,所以保持了相对位置不变
可视化网站
Merge Sort visualize | Algorithms | HackerEarth