算法学习之快速排序

2021-05-25 约 2741 字预计阅读 6 分钟

本文是学习排序系列的第四篇，主要介绍较为常用的排序算法：快速排序

前文学习了归并排序，该排序算法采用了分治(divide and conquer, D&C)的思想，我们可以使用递归对输入序列进行排序。但是归并排序与输入序列的有序程度无关，并且需要额外创建线性的空间，这对于数据规模较大的场景不是很友好。

本文要学习的快速排序同样也是基于分治思想的排序算法，相比于归并，快排的空间复杂度为常数级别，在C中，sort方法的底层实现的原型就是qsort快速排序~

注：本文的排序算法默认升序

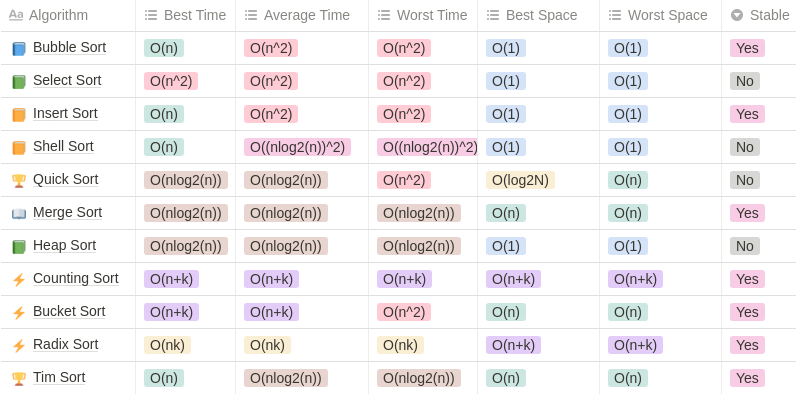
0. 常见排序算法性能对比

再贴一张常见排序算法的性能对比，方便查看~

1. 快速排序

快排是使用分治思想的排序算法，其巧妙地使用哨兵节点(pivot)，递归地将待排序的序列分为大于pivot和小于pivot两部分，进而达到分而治之，化大为小的目的。快速排序就是个二叉树的前序遍历

排序的简化情况

因为快排使用了递归的方法，所以为了明确递归思路，我们先对排序任务进行简单的剖析。

如果待排序的序列长度小于2，那么可以直接返回
如果待排序的序列长度等于2，那么比较两个元素即可
如果待排序的序列长度大于2，可以递归到小于等于2的情况

以上就是递归的想法雏形，其实递归的终止条件就是将大问题简化，简化到极端的情况，进而使用简化来反推复杂情况。

如何递归且O(1)？

前面说过，归并排序同样使用了分治与递归，但是空间复杂度为O(N)，所以快排应该如何将空间复杂度降低为常数级别的呢？

快排的思路就是原地分组，通过定义一个哨兵节点来实现。具体操作是将所有元素与哨兵节点的值相比较，小于哨兵节点的放在左侧，大于哨兵节点的放在右侧，这样逐层递归，就完成了排序的过程。

如下图所示，展示的是两次递归完成排序的过程，每次都取第一个元素为哨兵节点：

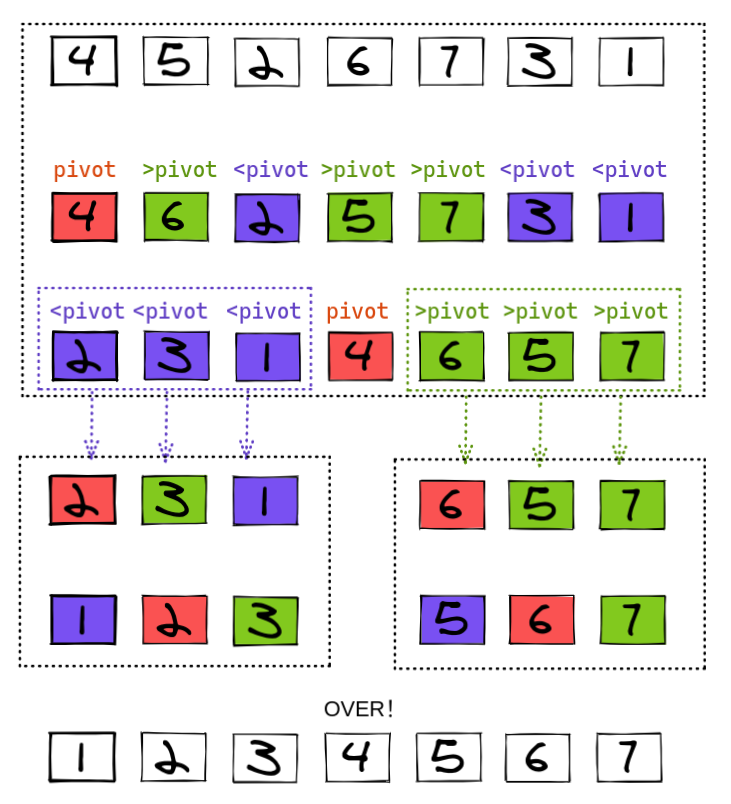
从上图可以发现，其实快排的基本思想可以认为是一个二叉树的模型，从上面不断地将当前数组分为两部分，直到达到递归终止条件。所以快排与归并排序的不同点在计算方式上也有体现，

归并是直接分组，然后从子问题开始处理，最后归并，是自下而上的算法，先处理子问题，再归并
但是快排是分组时就进行比较，一直到子问题无法继续划分，这时数组就排序完成了，是自上而下的算法，快速排序通过哨兵节点以及原地分组的方式，解决了归并排序中的内存占用

快速排序初版

根据上述思路，我们可以总结一下算法步骤

确定递归终止条件，也称为 base case

这里的终止条件是排序数组为空，否则继续向下递归
确定哨兵节点

为了简单容易理解，这里先将哨兵节点设为输入数组的第一个元素
根据哨兵节点进行递归排序

此时我们可以宏观地将数组分为两部分，比pivot小的，比pivot大的，与pivot相等的。分组完毕后，我们就可以调用自身进一步地对比pivot小的以及pivot大的两组进行再一次的划分，直到达到终止条件。

python版本代码如下

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


def quicksort(nums: List) -> List:
    def sort(nums):
        if nums == []:
            return []
        pivot = nums[0]
        nums = nums[1:]
        left = sort([num for num in nums if num <= pivot])
        right = sort([num for num in nums if num > pivot])
        return left + [pivot] + right

    return sort(nums)

复杂度分析

递归时间以及空间复杂度计算方式如下：

时间复杂度 = 递归调用栈深度 × 每次递归操作次数空间复杂度 = 递归调用栈深度 × 每次递归开辟的空间

所以为了分析递归的复杂度，我们需要确定递归调用栈的深度。

那么仔细思考一下，其实上述代码中的递归调用栈的深度是不确定的，因为我们的哨兵节点与其余元素的大小关系未知，我们可以分两种情况讨论，设待排序序列长度为N

最好情况，每次的哨兵节点都恰巧是当前序列的中位数，那么我们每次都可以完美地将输入序列分成近乎均等的两部分，这时的递归调用栈的深度为log2(N)，每次递归操作次数为N，开辟空间为常数级别。

那么时间复杂度就是 O(Nlog2(N))，空间复杂度为O(log2(N))
最坏情况，每次的哨兵节点都恰巧是当前序列中的极值，要么极大要么极小，这时我们的分治处理模型就从二叉树退化成了一维的结构，对应的递归调用栈深度为N，每次递归操作次数为N，开辟空间为常数级别。

那么对应的时间复杂度为O(N^2)，空间复杂度为O(N)

由此可见，上述快速排序可以称之为乞丐版，因为它不能很好地控制复杂度，所以我们可以进一步地改进，改进方案就是哨兵节点的选取。

优化方案：动态选取哨兵节点[双指针]

想要尽可能地分组均匀，哨兵节点的值应该尽可能地接近当前数组的中值

目的已经很明确了，就是要在当前数组中，遍历一遍，然后选取哨兵节点，我们可以使用双指针的方法来完成这个任务。

先假定基准值是数组中的第一个元素
定义两个指针left和right，分别指向第二个元素以及最后一个元素，规定left只能向右移动，right只能向左移动，且left不能超过right

(这里再说明一下双指针的作用，左指针负责维护一个小于基准值的区间，右指针则负责维护一个大于基准值的区间)
右指针先向左移动，每移动一位，都和基准值比较，如果遇到比基准值小的元素，停止，反之继续移动。移动左指针，同样边移动边比较，直到遇到比基准值大的元素，停止，与右指针交换位置(为了保证各自维护区间的元素值符合预期要求)
重复3直到左右指针相遇，将相遇位置的元素与基准值交换位置

这里借用袁厨的动图来可视化整个过程，侵删哈

经过以上过程，基准值所在的位置就是我们想要的哨兵节点，这时哨兵节点左侧都是较小元素，右侧都是较大元素，当前区间分组完毕！继续进行下一次递归的分组即可

python代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


def quicksort(nums: List) -> List:
    def partition(arr, left, right):
        base = left
        while left < right:
            while left < right and arr[right] >= arr[base]:
                right -= 1
            while left < right and arr[left] <= arr[base]:
                left += 1
            nums[left], nums[right] = nums[right], nums[left]
        nums[base], nums[left] = nums[left], nums[base]
        return left

    def sort(nums, start, end):
        if start >= end:
            return []
        pivot = partition(nums, start, end)
        sort(nums, start, pivot-1)
        sort(nums, pivot+1, end)

    sort(nums, 0, len(nums) - 1)
    return nums

优化后复杂度分析

如果不考虑极端情况的话，时间复杂度为O(NlogN)，空间复杂度为O(log2N)

但是不妨想一下，尽管我们使用双指针来优化了哨兵节点的选取，从而使每次哨兵节点的选择都尽可能靠近中间，但是如果输入的序列原本就是顺序或者倒序，那么退化的问题依旧会存在，所以极端情况下，时间复杂度依旧是O(N^2)，空间复杂度依旧是O(N)

为了解决上述问题，一般来讲都会将输入的序列进行打乱（shuffle），如果输入的序列规模很大，那么其实也可以尝试下随机选取一个哨兵节点，平均下来的时间复杂度是最优的。

稳定性分析

不稳定，因为分组时会发生随机的数据交换，从而导致值相同的元素相对位置变化

总结

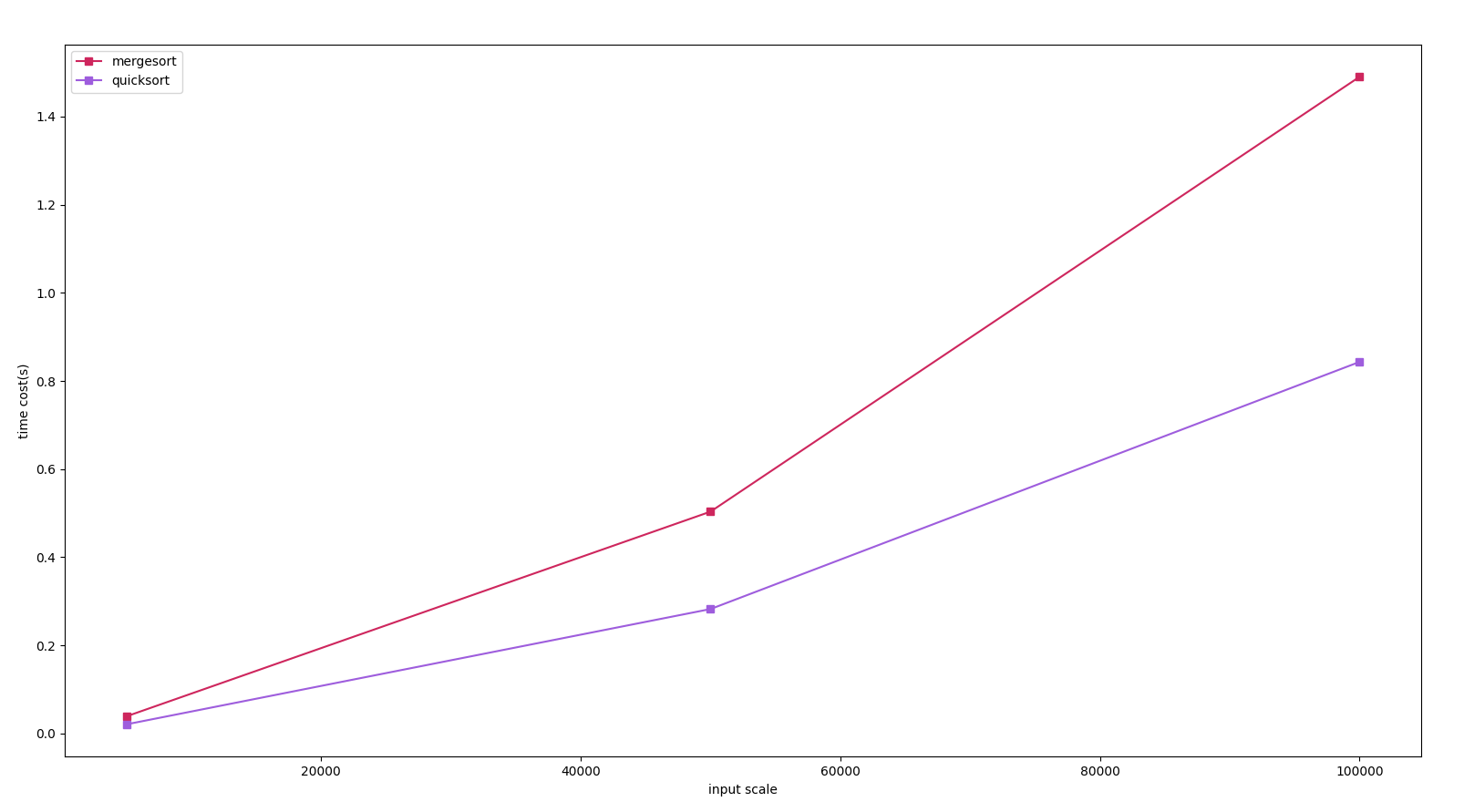
快速排序一般比归并排序要快
快速排序是不稳定的，因为在分组时会发生随机的数据位置交换
上述优化过后的快排代码针对数组中大量重复数据的情况效果不是那么地好(比如从0-200范围内随机选取50000个数值，快排的速度可能比希尔排序还慢，更别说归并排序了)，如果重复数据较多，可以单独处理

最后，贴一张快排和归并排序耗时比较的图~

目录