论文阅读18 Focal SparseConv
本文是CVPR2022的oral,也是旷视以及港中文贾佳亚老师团队的合作工作。主要是对稀疏卷积的改进,通过预测卷积核中每个位置的特征对输出的贡献程度,定义了一种重要性分数,然后利于阈值截取满足条件位置的特征。等同于标准稀疏卷积以及子流形稀疏卷积的中间版本。
简介
- 论文:《Focal Sparse Convolutional Networks for 3D Object Detection》
- 作者:Yukang Chen, Yanwei Li, Xiangyu Zhang, Jian Sun, Jiaya Jia
- 机构:CUHK, MEGVII, SmartMore
- 论文水平:CVPR 2022 oral
- 关键词:Sparse Convolution && 3D Object Detection
- 论文链接:paper code
TL;DR
摘要
非均匀 3D 稀疏数据,例如不同空间位置的点云或体素,对3D目标检测任务的贡献程度不同,无论是标准还是子流形稀疏卷积均如此。
本文引入了两个新的模块以增强稀疏卷积,他们都基于可学习的位置重要性预测。这两个模块分别是Focals Conv以及其融合了多模态的变体Focals Conv-F。这两个新模块可以简单地替换现有稀疏卷积中的模块,并且支持端到端地训练。
本工作验证了:稀疏卷积网络中,可学习的空间稀疏性对于3D目标检测至关重要,并且我们在KITTI、nuScenes以及Waymo数据集上通过大量实验验证了方法的有效性。我们模型的标注版本在nuScenes测试集上优于所有的现有工作。
讨论
对于三维数据,如激光雷达点云,其体素化后通过稀疏卷积提取特征的操作已经被研究学者们广泛应用,但是他们仍然具有一些显著的缺陷。
我们可以将常见的稀疏卷积分为两类,一类是标准的稀疏卷积,其计算卷积输出时将所有卷积核覆盖的非空元素作保留,这等同于将原有的稀疏特征做了膨胀操作,并且显著增加了计算量,导致一般只能应用在下采样后的特征图上。此外,对于检测任务而言,检测器需要显著地区分前景目标和背景,而这种标准的稀疏卷积则是实现了对原始稀疏数据的平滑滤波,这会破坏前景目标的显著性。
另一类稀疏卷积是子流形稀疏卷积,其只保留卷积核中心对应特征非空的元素,因此不会破坏原始稀疏特征的分布信息,并且不会引入过多的计算负担。但是由于仅当卷积核中心覆盖非空元素时卷积才起作用,这可能丢失必要的上下文信息,尤其是一些空间分布上不连续的特征之间的信息流。
因此,上述两种常见的稀疏卷积均存在一些限制,而这些限制本质上源于卷积的特性,所有输入的特征被卷积核等同对待,并没有区分各自位置上的信息差异性,这适用于2D稠密的图像卷积,但是针对于三维空间离散的特征分布,卷积的这一特性是无法解决点云数据的非均匀性以及稀疏性的。另一方面,现有的很多工作均关注于ROI的特征提取以及输出头的网络结构设计,但是底层特征在主干网络中的提取同样值得关注。这就是本文的动机所在。
主要贡献
- 分析了现有稀疏卷积的局限性,并提出了一种基于位置重要性的改进方案Focals Conv
- 提出了一种多模态的Focals Conv-F,通过简单轻量的的网络结构提取图像特征,并且与点云特征融合,简单高效。
- 大量的定量以及消融实验验证了方法的有效性。
方法框架
通用的稀疏卷积结构
给定输入的特征为$X_p$ ,通道数为$C_{in}$ ,那么使用一个卷积核对位置 $p$ 处的特征进行特征计算,卷积核的尺寸为 $\mathrm{w} \in \mathbb{R}^{K^{d} \times c_{\mathrm{in}} \times c_{\mathrm{out}}}$ ,那么普通卷积的处理公式为:
$$ \mathrm{y}{p}=\sum{k \in K^{d}} \mathrm{w}{k} \cdot \mathrm{x}{\bar{p}_{k}} $$
其中$k$ 枚举了$K^d$ 范围内的所有位置,$K^d$ 其实就是卷积核的大小范围,$\bar{p}_{k}=p+k$ ,比如$p=(1,1)$,$K^d$ 表示一个二维的 $3x3$ 的卷积核,那么 $k$ 的取值范围就是$(-1,-1),(-1,0),,,(1,1)$ ,所以上述公式等同于特征图上的特征与卷积核参数按位相乘再相加的过程。
而对于一些卷积的变种,同样可以根据修改上述公式实现,比如:
- 图像数据等稠密输入的卷积结构则是对应 $p \in \mathbb{Z}$
- 当$\bar{p}{k}$附带一个可以学习的偏置 $\Delta\bar{p}{k}$ ,那么就变成了可变的感受野,即deformable conv
- 如果卷积核 $\mathrm{w}$ 被一组系数加权,形如$\sum{\alpha}_{i}\mathrm{w}^{i}$ ,那么就变成了dynamic conv,可以进一步调整卷积核每个位置参数的权重。
- 如果使用注意力mask对输入特征图$x$做加权,那么就是input attention mask
现有两种稀疏卷积结构分析
而对于稀疏卷积,位置$p$不再属于密集的离散空间$\mathbb{Z}$ ,输入和输出的特征空间也分别放宽到$P_{in}$和$P_{out}$,二者均为稀疏离散的位置集合,因此稀疏卷积的公式转变为:
$$ \mathrm{y}{p\in{P}{out}}=\sum_{k \in K^{d}(p,{P}{in})} \mathrm{w}{k} \cdot \mathrm{x}{\bar{p}{k}} $$
$K^{d}(p,{P}_{in})$ 是 $K^{d}$ 的子集,只包含那些非空的位置,这也符合稀疏卷积的定义。
此外,前文同样说过,现有的稀疏卷积包含两种形式,分别是标注稀疏卷积以及子流形稀疏卷积,二者的唯一区别在于界定输出的规则不同。
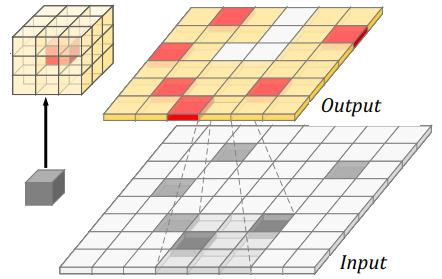
- 对于标准稀疏卷积,输出 $P_{out}$ 包含了所有的以 $P_{in}$ 为中心,$K^d$ 为边界的位置坐标,这种结构的稀疏卷积,任意卷积核覆盖到的非空位置均存在输出,如下图所示
 可以看到,输出的特征图将输入的稀疏特征做了膨胀,更加稠密的特征会带来额外的计算成本,此外,本文凭借实验结果发现,这种方案同样会降低原始数据的前景锐化程度,等同于滤波平滑操作,而这对于极度依赖前景特征的检测任务来说是很不友好的。
可以看到,输出的特征图将输入的稀疏特征做了膨胀,更加稠密的特征会带来额外的计算成本,此外,本文凭借实验结果发现,这种方案同样会降低原始数据的前景锐化程度,等同于滤波平滑操作,而这对于极度依赖前景特征的检测任务来说是很不友好的。 - 对于子流形稀疏卷积,输出应满足 $P_{out}=P_{in}$ ,因为此种卷积只有当卷积核中心覆盖非空特征时才计算输出,这使得输出的特征图非空元素与输入特征图等同,如下图所示
 这种方式避免了引入额外的计算成本,但是却可能丢失一些包含上下文连续信息的特征流,输出特征图的感受野受到了离散特征的限制,可能会导致模型表述能力的下降。
这种方式避免了引入额外的计算成本,但是却可能丢失一些包含上下文连续信息的特征流,输出特征图的感受野受到了离散特征的限制,可能会导致模型表述能力的下降。
本文提出的方案
上述两种稀疏卷积的方案,对于输出 $P_{out}$ 的定义都是静态的,而这种的一般无法cover不同稀疏程度的 $P_{in}$。因此,本文实现了对输入 $P_{in}$ 稀疏程度自适应的动态感受野设定,以决定不同的输出 $P_{out}$ 。
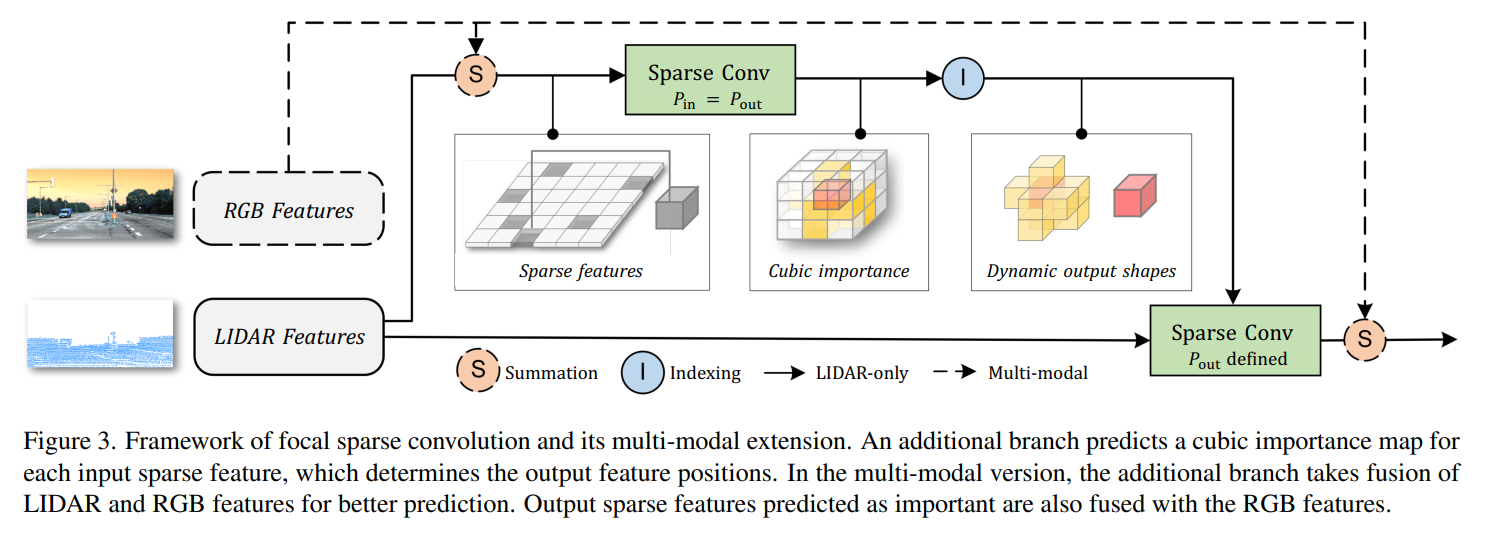
Focal Sparse Convolution
所谓的Focal,是指让网络凭借不同位置特征的重要程度有所取舍,重点关注那些较为重要的特征,从而动态地决定输出 $P_{out}$ ,对应的公式为:
$$P_{\mathrm{out}}=\left(\bigcup_{p \in P_{\mathrm{im}}} P\left(p, K_{\mathrm{im}}^{d}(p)\right)\right) \cup P_{\mathrm{in} / \mathrm{im}}$$
具体而言,衡量重要性以及动态决定输出的过程可以分为三个步骤,如下:
- cubic importance prediction 由于是针对三维点云数据的体素化结构,所以预测的重要性是立方级别,对输入特征 $P_{in}$ 的每个位置 $p$ 均预测一个立方体大小的重要性图 $I^p$ ,其形状尺寸与稀疏卷积的卷积核大小 $K^{d}$ 一致。 重要性 $I^p$ 的学习则是通过一层子流形卷积加上sigmoid函数得到,后续的两个步骤均基于 $I^p$
- important input selection 根据 $I^p$ 以及输入的 $P_{in}$ ,确定一个 $P_{in}$ 的子集 $P_{im}$ 表示相对重要的位置信息,计算方式为 $$P_{\mathrm{im}}=\left{p \mid I_{0}^{p} \geq \tau, p \in P_{\mathrm{in}}\right}$$ 其中, $I^p_{0}$ 是 $I^p$ 的中心,$\tau$ 是人工设定的超参数,表示截取重要性的阈值。通过调整这个阈值为0或1,可以转化为标准或子流形稀疏卷积。 而除了设定阈值,也可以取TopK个较为重要的位置作为输出。
- dynamic output shape generation 根据 $P_{im}$ 确定动态输出的卷积核 $K^d_{im}(p)$ ,计算方式为: $$K_{\mathrm{im}}^{d}(p)=\left{k \mid p+k \in P_{\mathrm{in}}, I_{k}^{p} \geq \tau, k \in K^{d}\right}$$ 其实就是对原始的 $K^d$ 中的每一个卷积核参数,判断对应位置的 $I^p$ 重要性是否大于阈值,保留满足条件的位置作为动态的特征图输出。
Fusion Focal Sparse Convolution
本文还提出了一种多模态的Focals Conv,其通过简单的网络结构提取图像特征并与点云特征对齐后直接按位相加,且实验证明此方案简单有效。
- 图像特征提取
不同于MVP[1]、PointPainting[2]等需要额外的后处理操作以融合点云图像信息,本文使用了轻量化的网络结构提取图像特征,主要可以概括为 一层conv-bn-relu以及maxpooling降低特征图尺寸为1/4,然后三层 conv-bn-relu的残差结构,最后通过一层MLP调整通道数量与稀疏点云特征对齐。得到的图像特征直接与点云特征相加。
- 特征对齐
考虑到点云特征通常会使用一些变换和增广操作使数据样本更加丰富,所以需要将图像特征与增广后的点云特征进行对齐。本文则是选择记录下所有的变换,然后将点云的稀疏特征进行反变换操作,以还原原始的点云基准。
监督信息的构建
本文对3D真值框中所有的体素特征构建了真值信息,并且使用Focal loss进行训练。
此外,另外一层监督信息间接地来自于检测任务的输出损失,通过将预测的重要性图 $I$ 作为加权分数与主干网络输出的特征做哈达玛积,可以使整个重要性预测模块变得可导,实现表明这种方案对于pedstrian与cyclist类别提升较为明显。
实验
定量实验
在KITTI、nuScenes以及Waymo数据集上均提供了定量的实验分析,其中Waymo的实验结果在补充材料中。
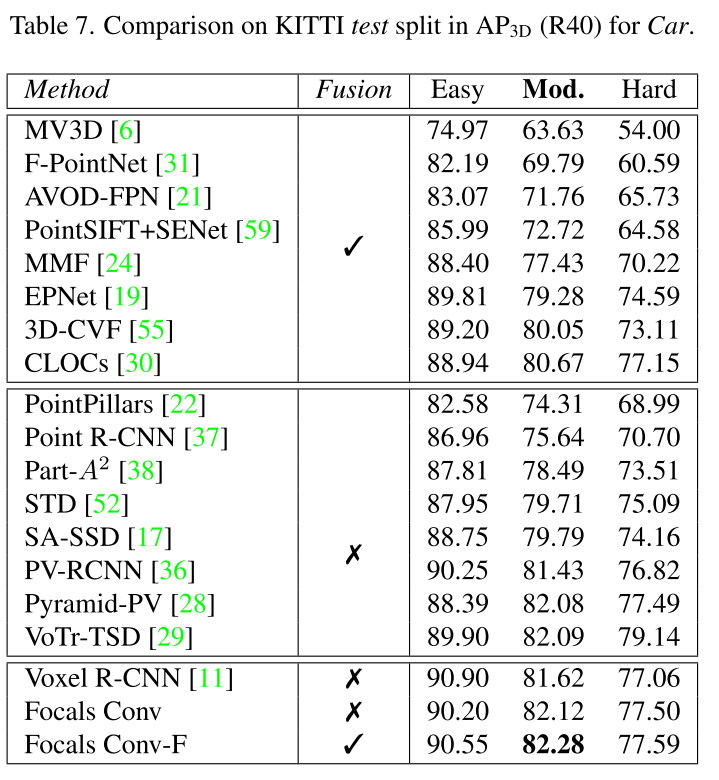
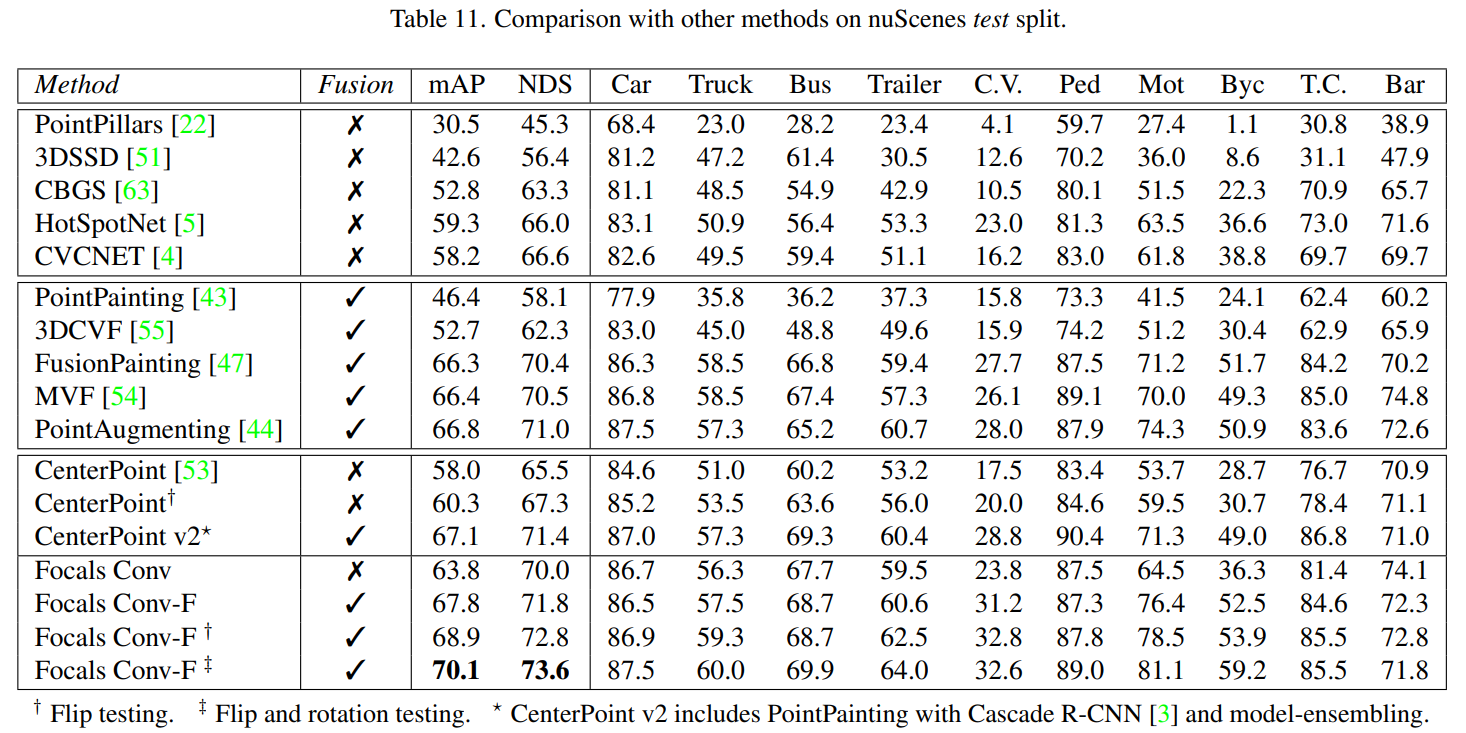
消融实验
本文的消融实验较为充分,如下:
- KITTI数据集上以PVRCNN为baseline,验证了Focals Conv的性能提升
- 对动态输出做消融,使用固定输出的形状替代
- 对重要性采样做消融,使用随机采样替代
- 对监督信息做消融
- 对应用Focals Conv的位置做消融
- 对重要性阈值做消融
- 对多模态做消融
- 对多模态的Fcals Conv应用位置做消融
对应的实验结果按顺序排列如下:
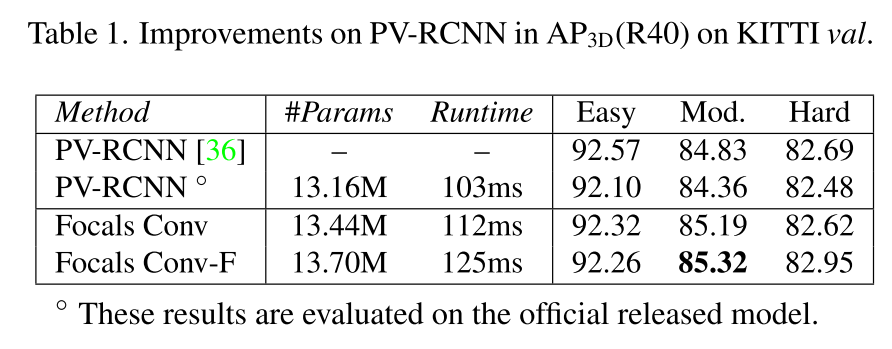
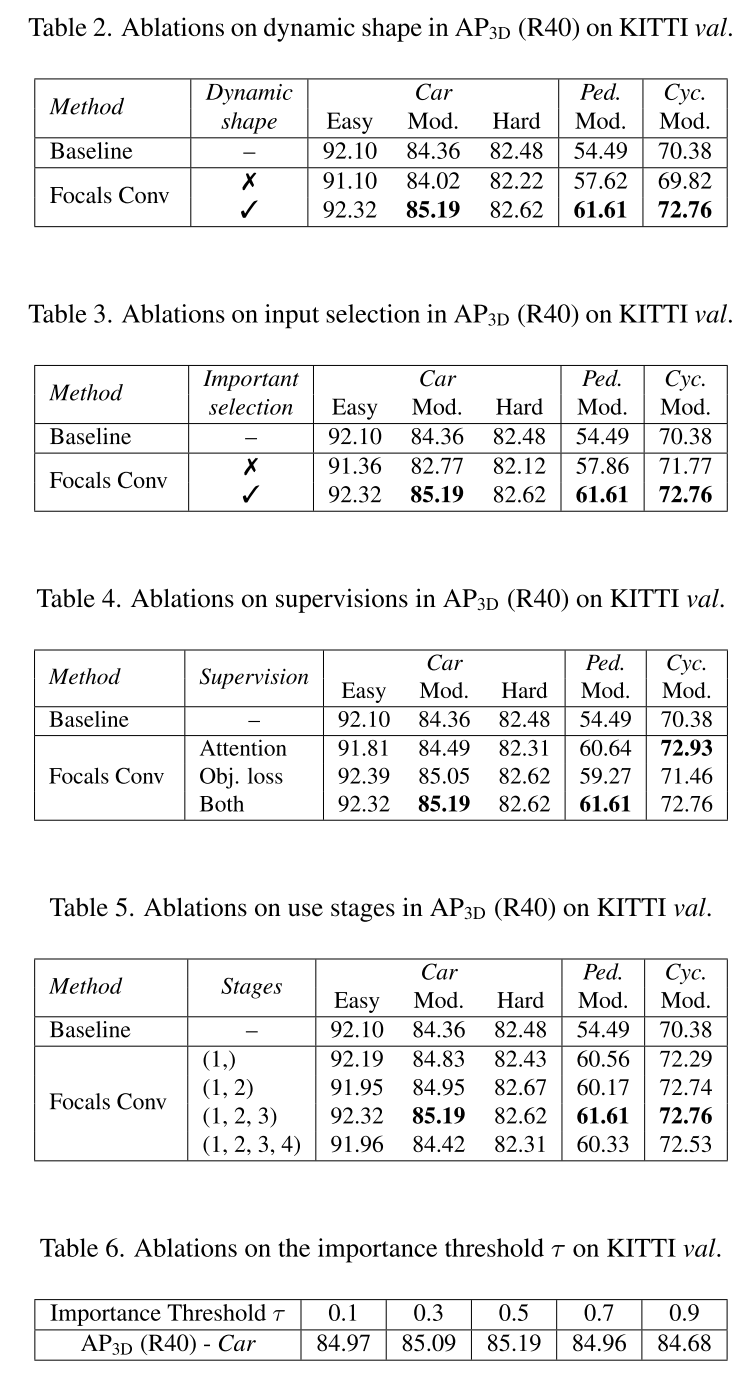
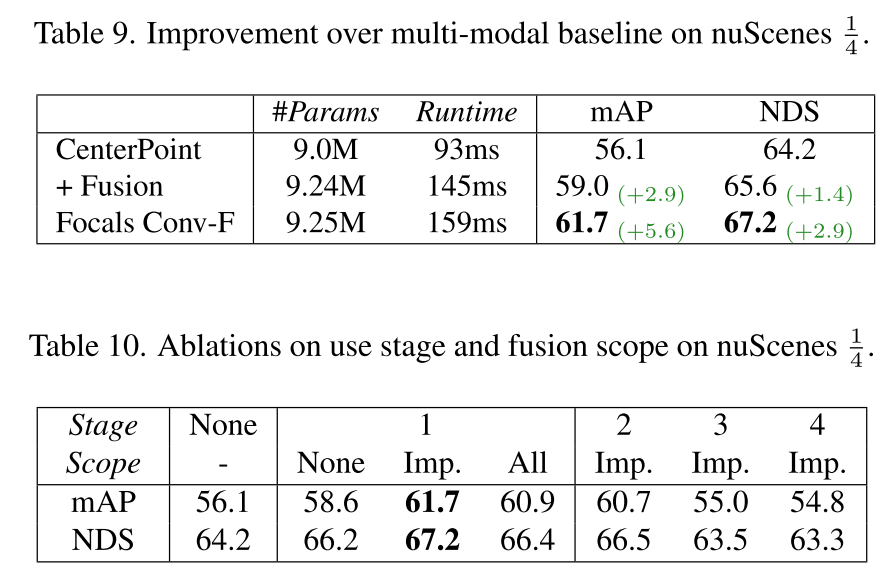
总结与思考
本文提出了一个Focal Sparse Conv和一个多模态扩展,它们简单有效并通过大量的实验验证了方法的有效性,作为对模块的改进工作,提出的两种模块均可以即插即用,直接替换稀疏卷积网络中对应的结构,简单高效。
参考文献
[1] T. Yin, X. Zhou, and P. Krähenbühl, “Multimodal Virtual Point 3D Detection,” NeurIPS 2021. [2] S. Vora, A. H. Lang, B. Helou, and O. Beijbom, “Pointpainting: Sequential fusion for 3D object detection,” Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., pp. 4603–4611, 2020.
 可以看到,输出的特征图将输入的稀疏特征做了膨胀,更加稠密的特征会带来额外的计算成本,此外,本文凭借实验结果发现,这种方案同样会降低原始数据的前景锐化程度,等同于滤波平滑操作,而这对于极度依赖前景特征的检测任务来说是很不友好的。
可以看到,输出的特征图将输入的稀疏特征做了膨胀,更加稠密的特征会带来额外的计算成本,此外,本文凭借实验结果发现,这种方案同样会降低原始数据的前景锐化程度,等同于滤波平滑操作,而这对于极度依赖前景特征的检测任务来说是很不友好的。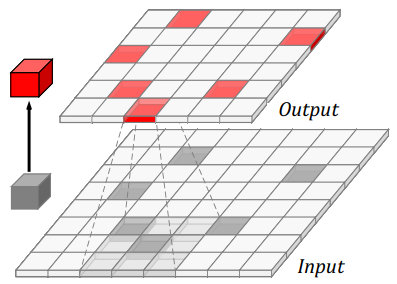 这种方式避免了引入额外的计算成本,但是却可能丢失一些包含上下文连续信息的特征流,输出特征图的感受野受到了离散特征的限制,可能会导致模型表述能力的下降。
这种方式避免了引入额外的计算成本,但是却可能丢失一些包含上下文连续信息的特征流,输出特征图的感受野受到了离散特征的限制,可能会导致模型表述能力的下降。