SLAM十四讲之第一讲 预备知识

第一讲主要介绍了SLAM的定义以及十四讲的组织关系，并且做了公式以及代码等风格约定。本文参考的版本是视觉SLAM十四讲的第二版。

SLAM的定义

SLAM： Simultaneous Localization and Mapping，中文译作同时定位与建图

SLAM具体是指：搭载特定传感器的机器人主体，在没有环境先验信息的情况下，在运动过程中，建立ego周围环境的模型，并估计ego自身的运动状态。视觉SLAM就是传感器是相机的SLAM方法。

SLAM的技术发展，其于1986年提出，至今已有近30年。

SLAM相关的背景知识包括：射影几何、计算机视觉、状态估计理论、李群李代数等。涉及到的编程库包括Eigen、OpenCV、PCL、g2o、Ceres等。

SLAM相关书籍包括：

• 《概率机器人》（ Probabilistic robotics）
• 《计算机视觉中的多视图几何》（ Multiple View Geometry in Computer Vision）
• 《机器人学中的状态估计》（ State Estimation for Robotics: A Matrix-Lie-Group Approach）

SLAM的框架结构

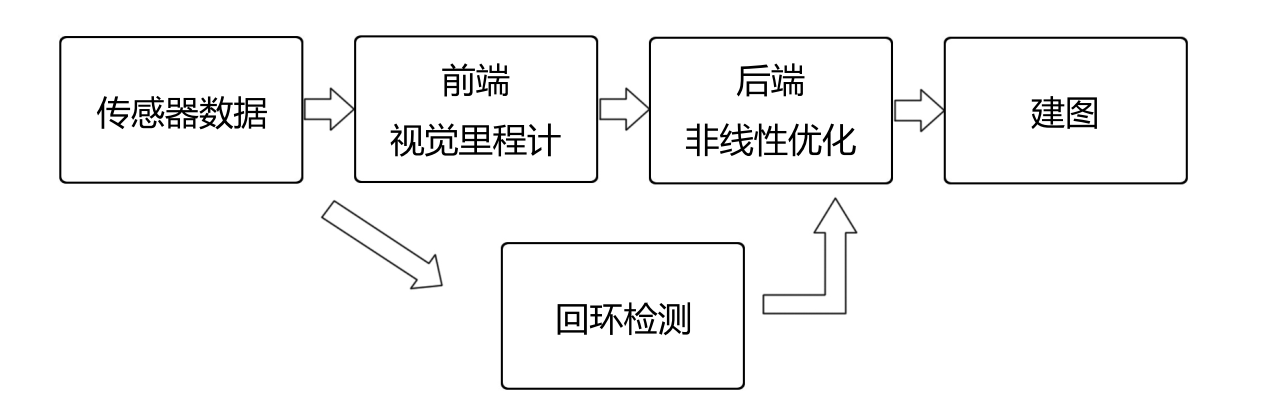
SLAM可以分为几个模块：前端里程计、后端优化、建图以及回环检测

注：这里仅分析视觉SLAM的相关内容

1. 前端里程计（前端）：
   1. 仅使用相邻几帧图像来估计相机的pose，叫做视觉里程计VO（此外也可以融合其他传感器，比如imu、wheel、lidar等，对应地就叫VIO、LVIO等）
   2. 一般包括直接法/特征点法
   3. 仅关注相邻时刻的运动！所以估计的也是相对的位姿，个人理解输出的是一种增量式的里程计，这就不可避免地存在drift，因此需要后端优化出对噪声进行处理（drift其实也可以理解成带有噪声的里程计）
2. 后端优化（后端）：
   1. 总体来说， 后端优化，要处理的是运动模型的过程噪声以及传感器观测的测量噪声，要从这些带有噪声的数据中估计系统状态，以及状态的不确定性—最大后验概率估计
   2. 前端相对于后端，要做的是对传感器进行参数化，对运动进行建模，然后将对应的状态和观测数据给后端，所以后端仅需要关注如何进行状态估计
   3. 早期的SLAM其实主要研究的就是空间状态的不确定性估计，也表示对运动主体自身和周围环境空间不确定性的估计，对应的主流方案也从滤波逐渐衍变为图优化。
3. 闭环检测（loop closure detection）
   1. 主要解决位置估计随时间偏移的问题，前提是ego经历过同一个位置，这样可以根据这种闭环的先验来纠正这一个闭环中的定位信息
   2. 比较重要的是如何判断闭环已经发生，这是一个判断两帧图像或两段图像相似性的任务
4. 建图
   1. 建图是机器人对外界三维环境的感知过程，相比于定位的估计自身位姿，建图是估计环境中的特定元素
   2. 地图的种类可以分为
      1. 度量地图
         1. 稀疏地图：特征点或线等元素（landmark）表示
         2. 稠密地图：所有能看到的，通常是像素投影到三维
      2. 拓扑地图
         1. 更强调低于元素之间的关系，是一个graph

SLAM问题的数学表述

按照上面的描述，slam可以包括定位和建图两个主要功能，定位是对机器人ego自身求解，建图则是对机器人周围环境求解，对应的数学问题都可以概括在一个框架内，如下：

$$ \left{\begin{array}{l} \boldsymbol{x}k=f\left(\boldsymbol{x}{k-1}, \boldsymbol{u}_k, \boldsymbol{w}k\right), \quad k=1, \cdots, K \ \boldsymbol{z}{k, j}=h\left(\boldsymbol{y}_j, \boldsymbol{x}k, \boldsymbol{v}{k, j}\right), \quad(k, j) \in \mathcal{O} \end{array} .\right. $$

其中，第一行表示运动方程，$\boldsymbol{x}_k$ 表示k时刻机器人的状态，k表示离散的时间序列，$\boldsymbol{u}_k$ 表示系统的输入，一般表示改变机器人运动状态的物理量，比如踩油门，$\boldsymbol{w}_k$ 表示运动的过程噪声，比如踩油门给机器人带来的加速度提升，存在的估计偏差。噪声的存在使得这个模型变成了随机模型。换句话说，即使我们下达“前进一米”的命令，并不代表机器人真的前进了一米。如果所有指令都是准确的，也就没必要估计什么东西了。

第二行表示观测方程，比如机器人看到了一个路标 $\boldsymbol{y}j$ ，那么就可以根据这个观测对运动方程估计的当前时刻k的状态 $\boldsymbol{x}k$ 进行估计，得到观测结果 $\boldsymbol{z}{k, j}$ 。同样地，观测到的路标也会有误差，所以引入观测噪声 $\boldsymbol{v}{k, j}$ 。

总得来说，这两个方程的求解，与具体的方程形式和噪声的分布形式有关：

• 方程可以分为线性和非线性
• 噪声可以分为高斯分布和非高斯分布

一般线性高斯的分布，其无偏的最优估计可以通过卡尔曼滤波求解，而非线性非高斯系统的求解，经历了几个过程：

1. 早期以EKF为主
2. 后来引入了粒子滤波，克服EKF的线性化误差以及噪声的高斯分布假设
3. 至今，则是以图优化为主流，因为计算平台的算力已经满足了优化所需的要求

十四讲内容安排

主要分为两部分，前面为相关基础，包括SLAM基础、三维空间运动、李群李代数、相机针孔模型以及非线性优化。

后面为特征点法以及直接法的视觉里程计、后端优化、位姿图、回环检测、地图构建、工程实践、技术展望等。

实践代码网址

https://github.com/gaoxiang12/slambook2

相关的学习资料

CMake tutorial CMake tutorial中文翻译