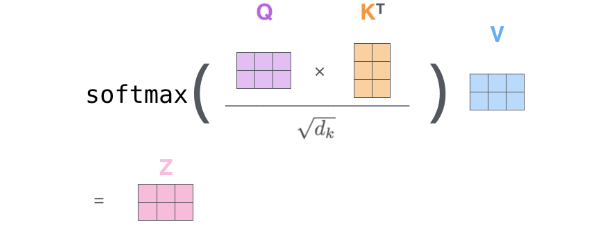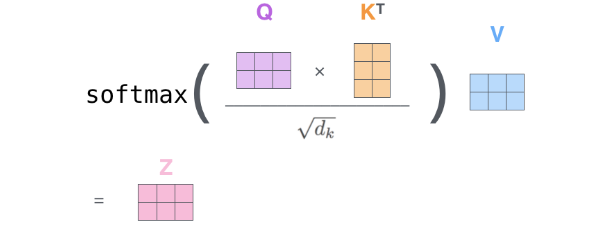Transformer之self-attention机制

jiayao 收录于学习笔记

2021-01-27 约 2778 字预计阅读 6 分钟

记录学习Transformer过程中的一些个人理解与思考

self-attention

1. 宏观理解

关于注意力机制，在此不做赘述，不过关于自注意力，可能还是先要从宏观上分析一下他是如何进行工作的

给定一个输入，可以是sequence或是图片或是点云，Transformer如何利用self-attention机制对输入进行深层次理解与学习？这其实就是self-attention的工作方式，总的来说，可以概括为

self-attention[自注意力层]是对输入信息做深层自我剖析，探究不同输入之间的相关性

在编码阶段，self-attention让每个当前向量“看”到其他位置向量的信息，进而编码成对应的特征

比如这张图片，在编码it时，self-attention就计算了it和其他单词向量之间的关系，进而让网络更好的编码it的特征

2. 微观分析

下面从细节上分析self-attention机制，以问题的方式记录

输入输出？

一般来说，self-attention的输入和输出一般都是特征张量，因为其主要作用是通过编码来对特征进行加权，除此之外还会涉及到Pos Encoding需要的位置信息等

如何对输入进行学习？

这里其实self-attention可以抽象地表达输入信息，如下图

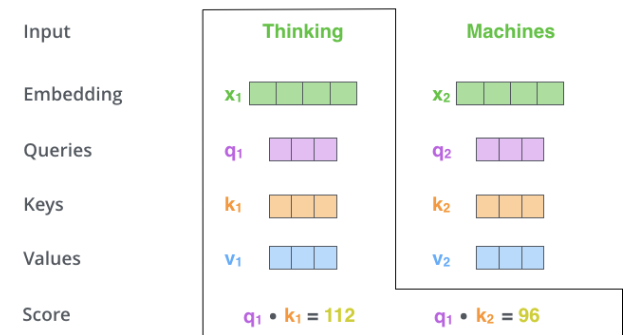
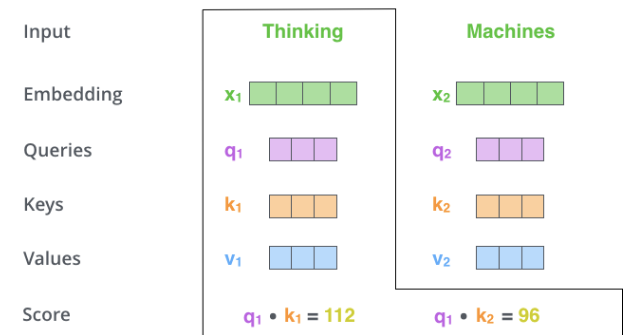
输入向量化（Embedding）

如果输入的是原始数据，那么需要将其向量化，进行 Embedding Vector 转换，其实就是转换成固定大小的特征向量，毕竟同一尺寸的特征对于网络比较友好
从三个角度学习输入的特征（Queries、Keys、Values）

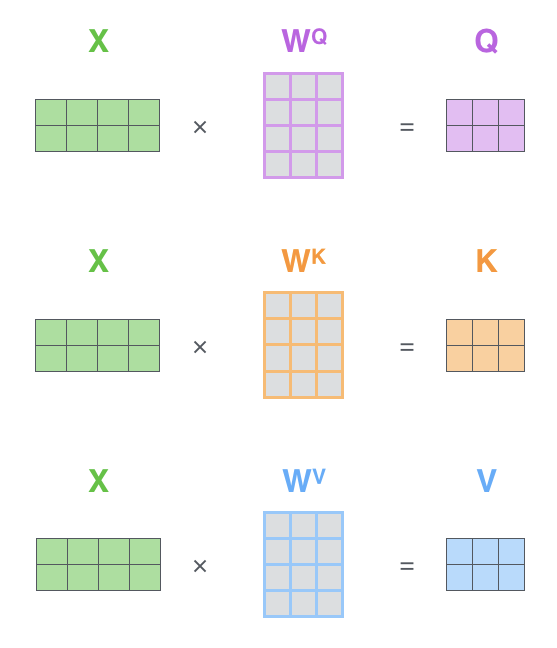
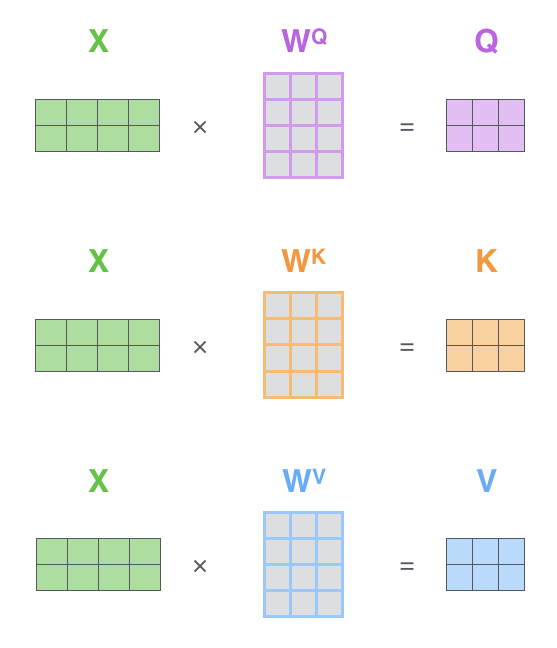
在self-attention中，可以理解为将输入拆解成三个参数，分别是Q K V，这个拆解是指输入的特征经过一个共享权值的网络层学习三个参数矩阵的具体值，如下图
- 其中Q代表着query，K代表Key，这两个向量的作用是对每个输入的特征向量做加权，让当前这个输入向量可以看到其他位置的特征信息，具体的做法就是，每个当前位置的Q与其他所有位置的K依次进行点积运算，得到的结果我们认为一定程度上代表了两个位置之间的相关性
- V的意义，我个人理解很大程度上是对输入的更鲁棒的表达，类似于卷积网络提取图片特征，这个V经过了矩阵Wv之后，其本身应该学习到了输入特征向量的一些高层次特征，这些特征较为鲁棒，所以可以更好的用来表达自身特征向量
计算self-attention的三步骤

那下面来说具体如何计算self-attention的，以及上面所有的Q、K、V是如何使用的
- 第一步，通过共享权值的参数矩阵W学习出三个矩阵Q、K、V
- 第二步，重复计算每个Q和所有K的内积，得到scaled inner product，并除以维度的开方以及做softmax归一化处理，这样就得到了每个向量的注意力加权得分，0-1之间
- 第三步，将每个向量的注意力加权得分与V进行点乘，也就是对每个向量进行注意力加权，在这个过程中，将Q和K计算得到的特征编码到了加权之后的V中
- 这里的自注意力，指的是，当前向量对全局的注意力，也可以理解为当前向量和全局所有向量的关联程度
self-attention与编码的关系

这里所谓的自注意力机制，就是在编码的过程中，增加全局线索，具体做法就是将当前向量和其他向量做计算，得到相关性，这个相关性经过正则化之后作为权重，分别乘上所有向量，最后将计算结果加和，其实上述过程就是在对当前向量编码的过程中，设定编码方式为计算当前向量与所有向量的相关度，然后加权求和，得到当前向量的特征编码。而体现全局线索的部分就是当前向量与所有向量计算相关性的操作
并行化加速的可能矩阵运算

注意，上述说的计算self-attention过程中，都可以通过矩阵来对运算进行表达，这也实现了加速的目的，相比于RNN的序列化计算，Transformer使用的self-attention就会快得多
一些问题
- 为什么学习q k v的参数矩阵是权值共享的？能否单独计算？
  
  这里的权值共享，指的是所有的输入都经过同样的W（包括Wq Wk Wv）来学习q k v，而如果权值不共享的话，应该是每个输入单独学习一个权重矩阵
- q k v的维度一定全部相同么？
  
  不是，是q和k计算relation之后得到的张量维度与v相同即可，因为relation function不仅有点乘这一种，也有相减
- 为什么q和k是做点乘的？这样可以很好的表达向量之间的相关性么？
  
  这种做法是通用的，此外，这种方式还有一种名字，叫做 scalar self-attention，这样计算的结果更多是对全局信息的一种表达，标量是对每个输入都一致的
  
  还有一种方案叫做 vector self-attention，具体做法就是将q和k做类似减法计算，然后得到的是每个特征向量都单独的结果，向量是每个输入得到的加权都不同
- 为什么需要做softmax？可不可以替换其他？功能要求是什么？
  
  这里的softmax其实可以概括为 normalization function，主要作用就是归一化，不过softmax是非线性的，这样可以是网络对于复杂的非线性系统拥有更好的表达
- 最终self attention的权重表示什么？atte与v一定要相乘么？系数相加不行么？
  
  最终的self attention权重表示的意义其实更多的取决于如何计算q和k之间的关系，如果是计算点乘，最终得到的是一个标量，那么这个权重更多是倾向一些全局信息的表达，如果是得到一个向量，那么每个权重不一致，则会更好的表达输入特征向量之间的相关性

Pos Encoding

位置编码层是为了让网络在另一个维度对输入数据进行理解，比如空间位置或序列信息

位置编码的概念就是在把原始数据向量化后，输入网络之前，让特征向量级联上一个表示位置信息或者序列信息的向量，这样可以让网络学习到一些序列化的信息

举个例子，如果没有位置编码，那么网络则更像是在计算组合，他不会考虑位置上的不同，注意这个位置是广泛的，可以是空间、时间等，那么这样的结果就是，输入一个语句，

1

你借了我100块钱

那么这句话也可能被翻译成

1

我借了你100块钱

所以加上位置编码，就可以让网络理解上下文信息的顺序特征，这是很重要的

提高网络感知信息的维度 — `Multi Head`

所谓的Multi Head机制，其实就是将每个特征向量原本学习到一组q k v，扩展到了N组，这样子分别计算注意力权重，那么每个输入的特征向量其实就得到了N个不同的加权之后的特征，经过网络的训练可以让这N个不同特征关注不同的点，这样更符合我们人类的注意力机制的方案

注意：

各个head之间，学习q k v参数矩阵的W矩阵也不相同
假如有N个head，那么最终得到的输出特征，其维度由N个head级联组成的，需要先将N个head进行concat，然后使用维度变换矩阵对其做维度对齐。
Multi-head Self-attention的不同head分别关注了global和local的讯息

参考

The Illustrated Transformer – Jay Alammar – Visualizing machine learning one concept at a time.

本来想自己翻译了，不过找到了对应的翻译版，链接如下

The Illustrated Transformer[翻译]

目录